《多面》 李家祥個展
ꕥ 展期 Duration:2009/10/01 (四) – 2009/10/25 (日)
ꕥ 開幕 Opening:2009/10/01 (四) 19:00
ꕥ 地點 Venue:台北數位藝術中心
ꕥ 地址 Address:111台北市士林區福華路180號;近捷運淡水線芝山捷運站二號出
ꕥ 展覽介紹
執行長的話
多面-限制下重組
如果將我們的視野從台灣畫同心圓逐漸擴大至全球,使我們從微觀到宏觀的角度觀看時,或許可以看到不同層面發生相似的事件、同一層面發生多樣的變化等等,都是在固定的行為軌跡上形成。倘若自身轉換視角觀看真理時,如同三D軟體由每一視窗看見不同面向,這對於事件的解釋將有所改變,然而真理顯得飄邈。在真實世界裡不僅擁有三維空間,「時間」形構成四維空間,它比起電腦運算的組合方式更為複雜,雖然人與人、與事、與物發生的種種無法全然透過科學精密計算,但行星的運轉、自然的演變、人類的行為皆遵循著法則而變動。科技和藝術的理性和感性之間,一直是我們在之中尋找的平衡點,台北數位藝術中心邀請李家祥藝術家展出「多面」主題個展,此展覽為台北數位藝術中心98年度重要的展覽之ㄧ,其理念反映了在限制條件下選擇不同面向的實踐方式。
「多面」-在數學幾何的公式中,相當理性地將點對點連成線、線與線構成面,李家祥透過數位計算過後,在公式裡的每條線、每一角度都是完全的絕對,沒有誤差的縫隙存在,最後卻以個人手工摺紙的方式呈現結果,此時丈量工具隱形為身體本能,透過摺紙過程對自我的丈量,同時也讓觀眾在他所設定的條件下摺出非數位化的作品,既不衝突又帶有趣味性。現場展示李家祥的摺紙作品,展覽場地設置了互動平台,觀眾可依照一層層步驟摺成與藝術家相同形狀的作品,而以此作為驅動互動程式的媒介,雖然經由參與者摺疊看似再複製的盒子,但每一個作品都存在著不同的意義,凸顯互動過程在此展覽理念的實踐的重要性。
黃文浩 Huang,Wen-Hao
﹉﹉﹉
創作概念
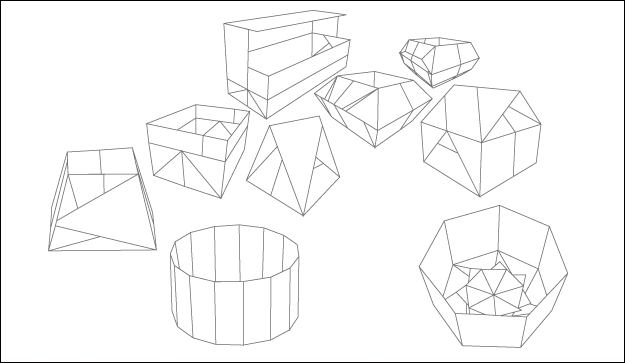
本次的作品「多面」,藉由探討在數學幾何公式中,一個多面體的形成,雖然有無限個點、線、面的方程式可供使用,看似可以無限制的產生,但是其實卻是要在多個限制條件的協調之下,才有可能建構出來。這反應出我們所看到的作品,雖然有很多的選擇性,但是最終的結果卻是在不同的限制條件中,經過取捨、調整及堅持,才能產生有特色的作品。「多面」代表著很多的面向,不論是形體上的多面、選擇上的多面、意見上的多面、呈現上的多面,都顯示出許多的可能性,但是最後卻是要在許多的限制中,才能得以具體實現。因此,將限制條件視為是一種創意的來源及思考方向的時候,其所能撞擊出的面向反而更多而且獨特。
在作品呈現上,利用摺紙盒的方式來傳達多面與限制的關係。在相同大小的紙張限制條件下,想要將增加紙盒高度,盒底面積必需要縮小;想要紙盒的容積越大,紙張的摺數及重疊數就不能太多;想要紙盒的邊數越多,摺出的每一邊的一致性就要更準確。原本認為的限制條件,反而引發更多的創意的可能性。
此外在互動的作品中,同樣以紙盒作為互動的介面,但是在展示台上並不預先放置紙盒,而是請參與者在現場親自摺出一個紙盒,就可以拿著紙盒在展示台上與數位影像進行互動,藉以傳達出參與者透過在現場親自摺紙盒,體驗為了要有更多面的呈現,隨之而來的限制,反而是真正的重點,而符合限制條件的紙盒才能產生互動。
﹉﹉﹉
創作論述
在數學幾何的公式中,要表示我們所處的空間的位置時,可以用3維的座標點 (x, y, z)來表示,此時可以表示的點有無限多個。當2個點連成一條線的時候,直線方程式可以表示為 ax+by=c,此時可以表示的直線也是無限多個。當3個點形成一個平面的時候,平面方程式可以表示為 ax+by+cz=d,此時可以表示的平面同樣是無限多個。看起來可以表示的點、線、面雖然有無限多個,但是若要形成一個有形物體,就必須要加上限制條件。例如:2個不同的平面的交集,結果就會形成一條直線,是一種限制條件。3個不同的平面的交集,結果就會形成個點,也是一種限制條件。再者,由多個面所形成的多面體,本身就是另一種限制條件的結果,越多面的多面體所需要的限制條件就更多。以立方體來說,由6個平面所組成,但是需要每3個平面一組,分別交集至8個端點,或是每2個平面一組,分別交集至12個邊線,才能計算出所需的6個平面的平面方程式,而這就是加上限制條件所產生的結果。不過如果再加上另外的限制條件,像是立方體的體積不能大於100,立方體的表面積要等於300。那麼,6個平面的大小彼此之間就會產生關連與牽制,例如:其中一平面的面積要較大的時候,其他的平面相對的就要有所取捨了。最後所形成的立方體形狀,便是在各個不同的限制條件下所產生的唯一的結果。
在數位藝術的創作中,最常用的呈現方式不外乎是影像與聲音。影像是由畫素所組成,而畫素本身可以用顏色來表示。我們可以使用的顏色,基本上是無限多個, 但是所使用的顏色必需是可見光的顏色,必需是電腦可以處理的顏色,此時可以使用的顏色就會有所限制,若是再加上需要的是可以讓人感到快樂的顏色,可以讓人焦慮的顏色等的限制條件時,可以使用的顏色就會更加受限了。最後所形成的數位影像,就是在多方的限制條件下所形成的結果。相對的,聲音是由頻率所組成,可以使用的頻率也是無限多個。但是所使用的頻率,必需是可以聽得見的頻率,必需是電腦可以處理的頻率,此時可以使用的頻率就會有所限制了。若是再加上所使用的頻率需要的是悅耳的,或是悲傷的,那麼可以使用的頻率就會有所限制了。而最終的聲音作品,就是在各個限制條件下所形成的結果。
在互動藝術中,常常會聽到有些創作者在介紹作品的時候,會提及因為基於技術可行性的限制、材料的限制、設備效能的限制、空間的限制、時間的的限制、經費的限制等等,各種的限制條件,最後才能產生獨特的結果。試想如果去除了所有的限制條件,那種克服限制條件所產生的創作喜悅,反而無法體驗到了,此時的無限制卻成了最大的限制。有時在合作的過程中,採納各種的意見固然是一種理想的狀態,但是最後要能完成工作任務,卻是要在適當的限制條件下,意見才會發揮實質的作用。
由以上的說明,可以發現當選擇性愈多的時候,甚至是無限的時候,並不能產生作品、形體等,只有加入不同的限制條件,並且各個限制條件彼此之間還要經過取捨,調整及堅持,如此才能產生有特色的作品。
「多面」代表著很多的面向,不論是形體上的多面、選擇上的多面、意見上的多面、呈現上的多面,都顯示出許多的可能性。但是最後卻是要在許多的限制中,才能得以具體實現。因此,將限制條件視為是一種創意的來源及思考方向的時候,其所能撞擊出的面向反而更多而且獨特。
ꕥ 作品介紹 1
邊角系列 Side Series
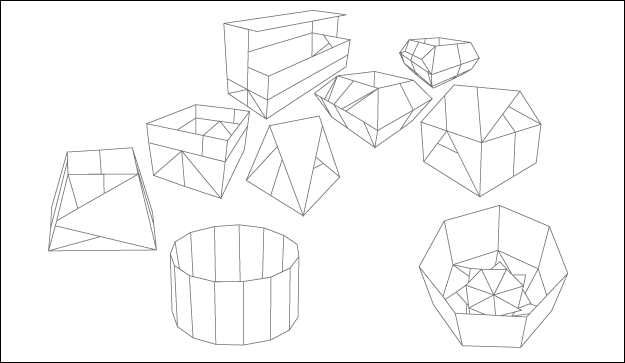
這個系列的作品利用將相同大小紙張的邊長進行等分作為邊角創意的來源。以一張紙的一個邊的邊長為準,分成多個等分,等分的越多,邊數就越多,相對的每個邊長的長度就越小,所得到的角度也越小,同時底面長度也會增加,但是不論等分的數量有多少,最後都要相交於一點才能完成。當等分的數量大到一個程度時,因為紙張厚度的關係,想要相交於一點就更加困難了。在此系列中,共有2件作品,邊角1號(8等分)及邊角2號(15等分),當邊長的等分決定時,底面積及邊角的大小,也就跟著確定了。
﹉﹉﹉
ꕥ 作品介紹 2
七邊形 Heptagon
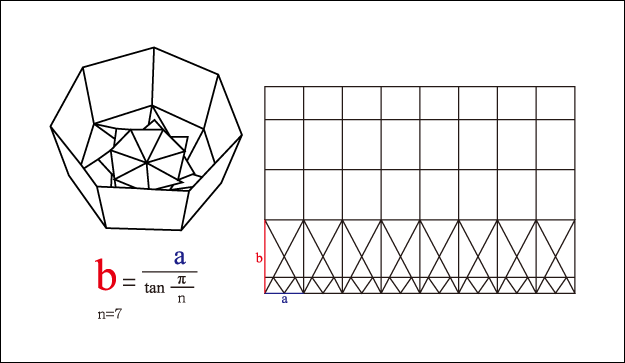
當對摺3次(x)後, 即可得到8等分, 其中一邊重疊, 就形成了7邊(n), 也就是n = 2x – 1, 當x=3時, n=7. 此外, 當等分的長度為a, 等分數量為n時, 所得到的底面長度(b)就是 b = a / tan(π/n), 當n=7時, b=2.1a, 以A4的紙為例, 長邊的長度是 297mm, b=2.1a, a=297/8=37.125, b=77.96, 原則上, 等分數量可以不斷的增加, 但是當n大於29時, 等分的長度就變成小於297mm/(29+1) =9.9mm, 對摺紙來說是有困難的, 這也是限制所在.
﹉﹉﹉
ꕥ 作品介紹 3
十五邊形 Pentadecagon
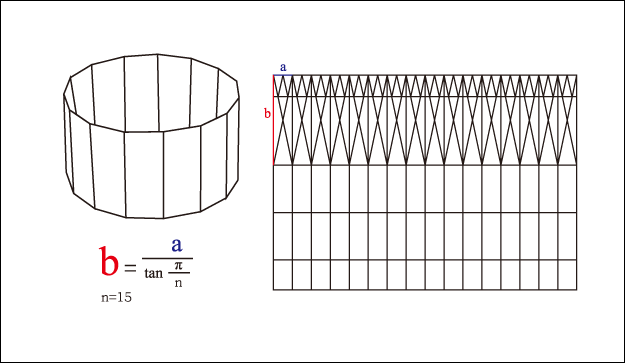
當對摺4次(x)後, 即可得到16等分, 其中一邊重疊, 就形成了15邊(n), 也就是n = 2x – 1, 當x=4時, n=15. 此外, 當等分的長度為a, 等分數量為n時, 所得到的底面長度(b)就是 b = a / tan(π/n), 當n=15時, b=4.7a, 以A4的紙為例, 長邊的長度是 297mm, b=4.7a, a=297/16=18.56, b=87.24, 原則上, 等分數量可以不斷的增加, 但是當n大於29時, 等分的長度就變成小於297mm/(29+1) =9.9mm, 對摺紙來說是有困難的, 這也是限制所在.
﹉﹉﹉
ꕥ 作品介紹 4
弧角系列 Arc Series
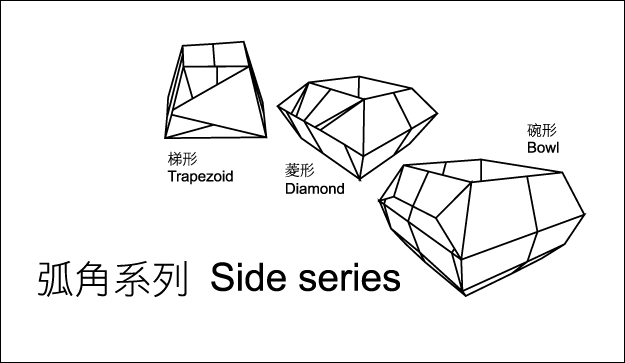
弧角系列 (梯形, Trapezoid)
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成2分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a為邊長b的1/4時, 所得到的高度h就是 (c – a), 也就是 h = c – (b/4), 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, h = (210/2) – (279/2/4) = 67.875mm
﹉﹉﹉
ꕥ 作品介紹 5
梯形Trapezoid
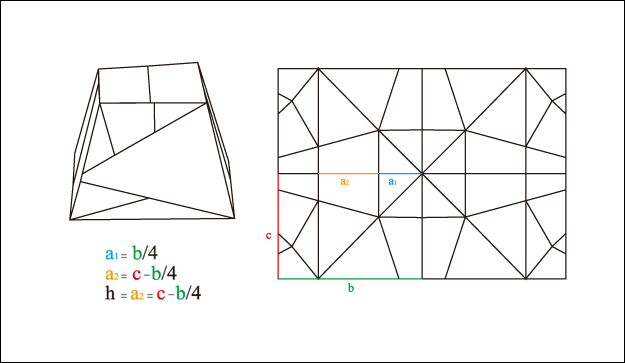
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成2分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a為邊長b的1/4時, 所得到的高度h就是 (c – a), 也就是 h = c – (b/4), 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, h = (210/2) – (279/2/4) = 67.875mm
﹉﹉﹉
ꕥ 作品介紹 6
菱形 Diamond
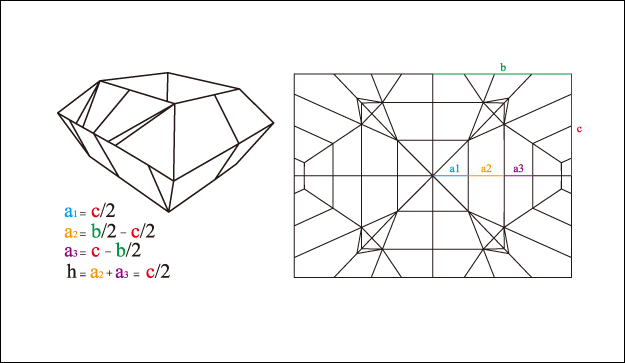
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成3分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a1為邊長c的1/2時, 分段長度a2 = (b/2) – (c/2), 分段長度a3 = c – (b/2), 所得到的高度h就是 a2+a3, 也就是 h = a2 + a3 = c/2, 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, a2 : a3 = 1 : 1.41, h = 210/2/2 = 52.5mm
﹉﹉﹉
ꕥ 作品介紹 7
碗形 Bowl
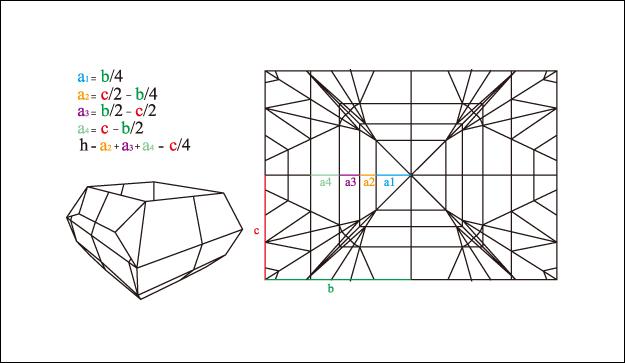
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成4分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a1為邊長b的1/4時, 分段長度a2 = (c/2) – (b/4), 分段長度a3 = (b/2) – (c/2), 分段長度a4 = c – (b/2), 所得到的高度h就是 a2+a3+a4, 也就是 h = a2 + a3 + a4 = c – b/4, 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, a2 : a3 : a4 = 1 : 1.41 : 2, h = 67.875mm
﹉﹉﹉
ꕥ 作品介紹 8
斜角系列 Oblique Series
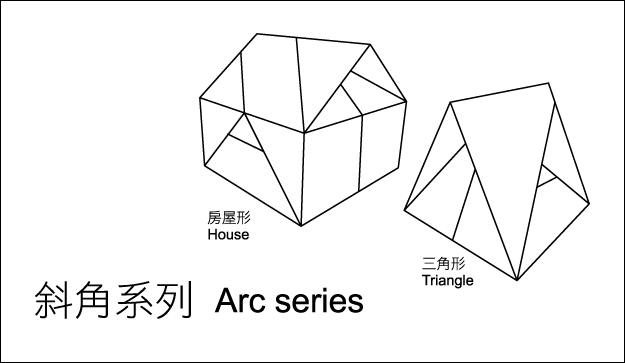
這個系列的作品利用將相同大小的直角三角形的中心線進行分段作為斜角變化創意的來源。以一個直角三角形的中心線為準,分成幾個分段後,將最上層分段的二邊線疊合在一起的時候,就會形成三角柱體了。當最上層的分段比例越大時, 三角柱體的斜角就會越尖,但是同時下層的高度及邊長就會減小。當最上層的分段比例減小到一個程度時,三角柱體的斜角就會越平,反而無法形成三角柱體。在此系列中,共有2件作品,斜角1號(2分段)、2號(3分段)。當中心線分段的比例決定的時候決定的時候,高度及斜角的大小,也就跟著確定了。
﹉﹉﹉
ꕥ 作品介紹 9
屋型 House
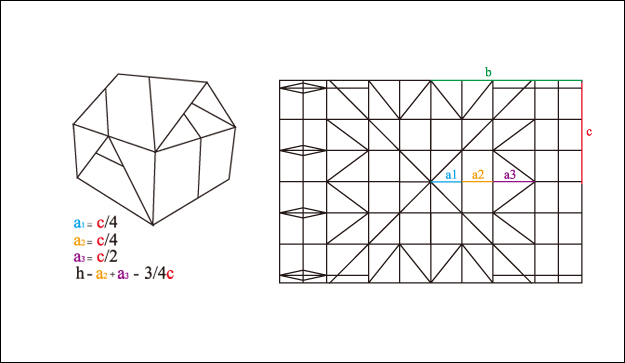
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成3分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a1為邊長c的1/4時, 分段長度a2 = c/4, 分段長度a3 = c/2, 所得到的高度h就是 a2+a3, 也就是 h = a2 + a3 = c*3/4, 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, a2 : a3 = 1 : 2, h = (210/2)*3/4 = 78.75mm
﹉﹉﹉
ꕥ 作品介紹 10
三角形 Triangle
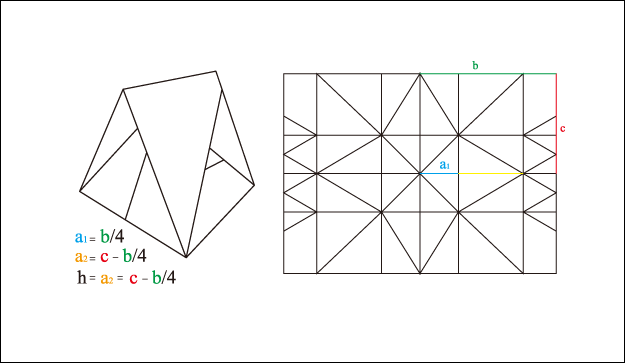
將紙張摺成三角基本形後, 以直角三角形的中心線進行分段, 當分成2分段時, 若2個邊長的長度分別為b及c, 底部的分段長度a為邊長b的1/4時, 所得到的高度h就是 (c – a), 也就是 h = c – (b/4), 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, b = 297/2, c = 210/2, h = (210/2) – (279/2/4) = 67.875mm
﹉﹉﹉
ꕥ 作品介紹 11
彎角系列 Bend Series
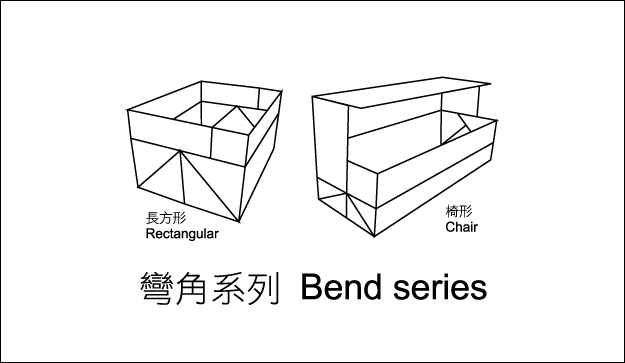
這個系列的作品利用將相同大小紙張的邊長進行分段作為彎角變化創意的來源。以一張紙的一個邊的邊長為準,分成多個分段,此時各個分段的數量及大小各不相同的,最後會形成一個長方體。當分段的數量越多,可以折彎的次數就越多,但是相對的,長方體的長, 寬, 高都會受到大小不等的影響,有可能是高減少,長增加,寬不變,也可能是任何未知的變化。在此系列中,共有2件作品,彎角1號(10分段)、2號(11分段)。當邊長的分段決定時,長方體的長、寬、高大小,也就跟著確定了。
﹉﹉﹉
ꕥ 作品介紹 12
長方形 Rectangular
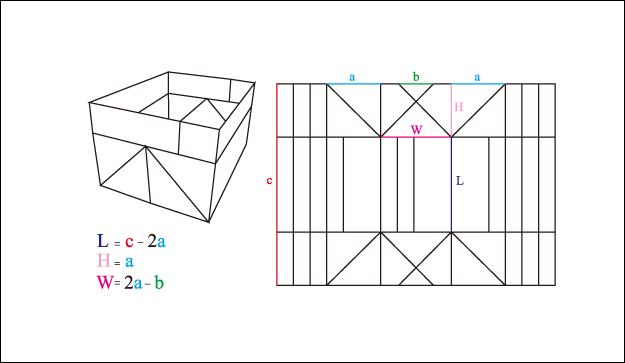
以紙張一個邊的邊長為準,分成多個分段,此時各個分段的數量及大小各不相同,其中做為高(H)的尺寸為a時, 底部的重疊區為b, 紙張的短邊的長度c時, 寬(W)的尺寸就是 (2a – b), 長(L)的尺寸就是 (c – 2a), 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, 當高的尺寸a = 297/6 = 49.5mm, 重疊區b = a/2 = 24.75mm時, 寬的尺寸就是 (2a – b) = 74.25mm, 長的尺寸就是 (c – 2a) = 111mm
﹉﹉﹉
ꕥ 作品介紹 13
椅型 Chair
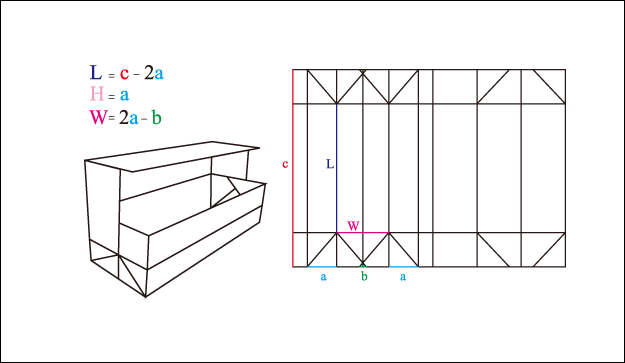
以紙張一個邊的邊長為準,分成多個分段,此時各個分段的數量及大小各不相同,其中做為高(H)的尺寸為a時, 底部的重疊區為b, 紙張的短邊的長度c時, 寬(W)的尺寸就是 (2a – b), 長(L)的尺寸就是 (c – 2a), 以A4的紙為例, 長邊的長度是297mm, 短邊的長度是210mm, 當高的尺寸a = 297/8 = 37.125mm, 重疊區b = a/4 = 9.28mm時, 寬的尺寸就是 (2a – b) = 64.97mm, 長的尺寸就是 (c – 2a) = 135.75mm
﹉﹉﹉﹉
摺紙動畫 Animation
| 作品名稱 | 作者 |
| 生命線/Eletvonal | Tomek Ducki |
| 輪廓/Silhouettes | Vincent Courbis-Poncet/Remi Despret/Jean David Solon |
| 墜落的天使/La chute de L’ange | Geoffroy Barbel Massin |
| 奧兒睡美人/La belle au bois d’or | Geoffroy Barbel Massin |
| 愛是什麼?/A quid ca sert l’amour? | Louis Clichy |
| 故事的主軸/Line histoire vertebrale | Jeremy Clapin |
| 在你懷裡/En tus brazos | Francois Xavier Goby/Edouard Jouret/Matthieu Landour |
| 蝴蝶/Le papillon | Antoine Antin/Jenny Rakotomamonjy |
| 圍牆背後/Le dos au mu | Bruno Collet |
| 生活記號/Signes de vie | Arnaud Demuynck |
| 卡里普索就是這樣/Calypso is like so | Bruno Collet |
ꕥ 藝術家講座
多面 Multi-Constrains 李家祥個展 藝術家講座
2009/10/1 20:00 地點: 台北數位藝術中心
講師 : 李家祥
內容 : 多面 創作過程分享
ꕥ 創作工作坊
多面 創作工作坊
本工作坊主要希望透過學習摺紙的活動參與,讓民眾可以利用親手摺出來的紙盒與數位影像進行互動,當民眾將紙盒放置在現場安排的展示桌上時,桌上的攝影像擷取紙盒的影像並投影在投影幕上,之後會從畫面中的紙盒上顯現出不同的幾何圖像,當民眾將紙盒從展示桌移走後,若再次放到展示桌上時,畫面中的紙盒上會顯現出另外的幾何圖像。
本次的摺紙教學主要以紙盒造形為主,紙盒是我們日常生活最常接觸的用品之一,而紙盒也是最常被大家拿來作為摺紙的練習,因為紙盒本身除了造形之外也兼具功能性,不過,在摺紙的過程中,只要稍為加入一些巧思,再平常不過的紙盒,也可以變化出許多的創意出來。
因此,利用紙盒作為民眾與數位影像互動的介面,是本次工作坊的主要目標,期望藉由大家熟知的摺紙,帶領民眾認識數位藝術。
主題:多面 創作工作坊
時間:2009.10/24 (SAT) 14:00
地點:台北數位藝術中心
講師:李家祥
學員人數:30人
目的:利用紙盒作為民眾與數位影像互動的介面,期望藉由大家熟知的摺紙,帶領民眾認識數位藝術。
講師簡介
李家祥
個人簡歷
李家祥,科技藝術工程師,國立台北科技大學機電科技研究所博士生。目前為台灣師範大學設計所駐校藝術家、台中技術學多媒體設計系兼任講師。主要的研究方向為網路互動介面整合與互動系統開發、數位內容創意加值、數位互動藝術創作、多媒體互動設計、無線網路應用、行動裝置應用、互動控制系統設計、創意學習內容設計、機電整合應用。
早期參與過工廠儀控系統程式設計,網站系統程式設計、數位內容管理系統開發及數位典藏專案。目前主要從事於數位藝術及互動藝術之教學推廣,以及互動系統開發之整合與應用,並多次擔任工作坊的授課老師,以及協同教學的工作。2003年與曾鈺涓合作並成立所以然藝術實驗室,實踐互動藝術創作。
ꕥ 活動紀錄
開幕茶會
時間:10/1 19:00
地點:台北數位藝術中心
藝術家講座
時間:10/0 20:00
內容: 李家祥老師談論多面創作過程
多面創作工作坊
時間: 10/24 14:00
內容: 李家祥老師帶領民眾以平易近人的摺紙漸進入純數位理論的數位藝術理論,
另外會以過程中產生的作品與互動桌產生有趣的互動.
 EXHIBITION
EXHIBITION

